Autour des angles
1. Généralités.
1.1. Quelques rappels de Sixième.
1.1.1. Définition d'un angle.
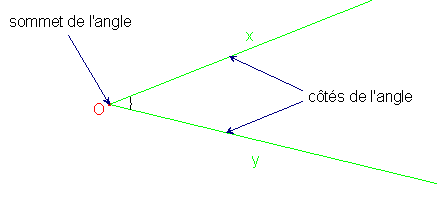
Définition : Un angle est formé de deux demi-droites de même origine. Cette origine est appelé le sommet de l'angle. Les demi-droites sont appelés les côtés de l'angle.
|
|
|---|
|
Angle
|
Remarque: Un angle se désigne toujours par trois lettres.
1.1.2. Mesure d'un angle.
L'unité de mesure des
angles est le degré (noté °). L'instrument de
mesure est le rapporteur. La mesure de l'angle
![]() se
note
se
note
![]() .
.
En général, on confond l'angle et sa mesure.
Exemple:
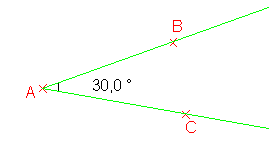
En
théorie, on écrit:
![]() .
.
En pratique, et par abus, on
écrit:
![]() .
.
1.1.3. Classification des angles.
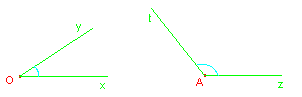
1.1.3.1. Angle rentrant. Angle saillant.
 |
 |
||
|
Angles saillants: Un angle saillant est un angle compris entre l'angle nul et l'angle plat (voir ci-dessous). La mesure d'un angle saillant est comprise entre 0° et 180°. |
Angles rentrants: Un angle rentrant est un angle compris entre l'angle plat et l'angle plein. La mesure d'un angle rentrant est comprise entre 180° et 360°. |
||
|
|
|
|
|
Remarque: La limite entre un angle saillant et un angle rentrant est l'angle plat (voir figure ci dessous)
1.1.3.2. Classification des angles saillants.
Un angle saillant peut être:
|
- un angle nul |
 |
La mesure d'un angle nul est de 0°. |
|
- un angle aigu |
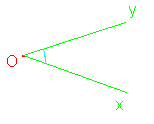 |
Un angle aigu est compris entre un angle nul et un angle droit. Sa mesure est donc comprise entre 0° et 90° |
|
- un angle droit |
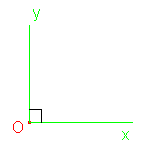 |
Un angle droit mesure 90° |
|
- un angle obtus |
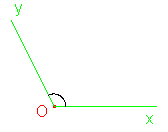 |
Un angle obtus est compris entre un angle droit et un angle plat. Sa mesure est donc comprise entre 90° et 180° |
|
- un angle plat |
|
Un angle plat mesure 180°. |
Remarque: Un angle saillant est donc un angle dont la mesure est inférieure ou égale à 180° et un angle rentrant est un angle dont la mesure est supérieure ou égale à 180°.
Un angle aigu a sa mesure comprise entre 0 et 90° et un angle obtus mesure entre 90° et 180°.
1.1.4. Bissectrice d'un angle.
Définition: La bissectrice d'un angle est la demi-doite qui partage un angle en deux angles de même mesure.
Exemple:
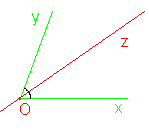
[Oz) est la bissectrice de
l'angle
![]() .
On a:
.
On a:
![]() .
.
Savoir
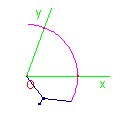
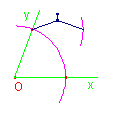
construire la bissectrice d'un angle avec un compas:
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
||||
|
|
|
|
|
|
|
|
||||
Remarque: Pendant toute la construction, on garde la même ouverture de compas.
Propriété (admise): La bissectrice d'un angle est l'axe de symétrie de cet angle.
1.2. Symétrique d'un angle par rapport à un point.
Propriété (admise): Deux angles symétriques par rapport à un point ont la même mesure.
Conséquence: Si deux droites sont perpendiculaires, alors leurs symétriques par rapport à un point sont perpendiculaires.
2. Des couples d'angles remarquables.
2.1. Angles opposés par le sommet.
Définition: On dit que deux angles sont opposés par le sommet lorsque:
ils ont le même sommet;
leurs côtés sont dans le prolongement l'un de l'autre.
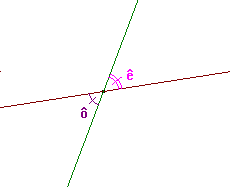
Propriété: Deux angles opposés par le sommet ont la même mesure.
2.2. Angles adjacents.
Définition: On dit que deux angles sont adjacents lorsque:
ils ont le même sommet;
ils ont un côté commun;
ils sont de part et d'autre de ce côté commun.
Exemple:
|
Les angles â et ê sont des angles adjacents |
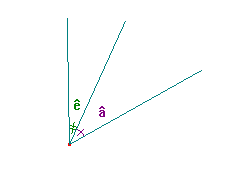 |
Contre-exemples:
|
ê et â ne sont pas adjacents car ils ne sont pas de part et d'autre du côté commun aux deux angles. |
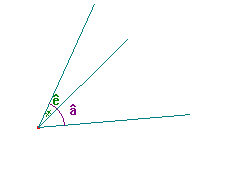 |
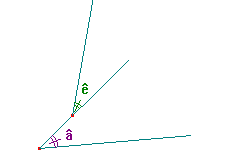 |
ê et â ne sont pas adjacents car leurs sommets ne sont pas identiques. |
2.3. Angles complémentaires. Angles supplémentaires.
2.3.1. Angles complémentaires.
Définition: Deux angles dont la somme des mesures est égale à 90° sont dits complémentaires.
Remarque: Deux angles complémentaires ne sont pas nécessairement adjacents.
Exemple:
2.3.2. Angles supplémentaires.
Définition: Deux angles dont la somme des mesures est égale à 180° sont dits supplémentaires.
Remarque: Deux angles supplémentaires ne sont pas nécessairement adjacents.
Exemple:
2.4. Angles et droites parallèles coupées par une sécante.
2.4.1. Définitions.
2.4.1.1. Angles alternes-internes.
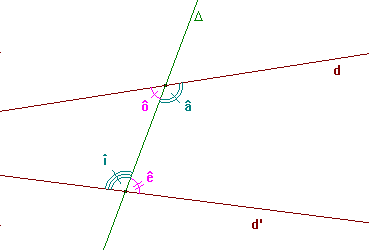
Sur la figure, les angles â et î sont des angles alternes-internes, ainsi que les angles ê et ô.
Deux angles alternes-internes sont tels que:
ils sont situés à l'intérieur de la bande de plan formée par les droites d et d'
ils sont de part et d'autres de
 .
.
2.4.1.2. Angles correspondants.
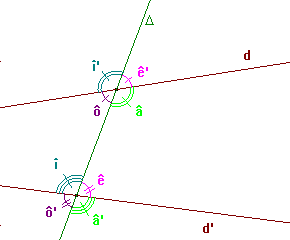
Sur la figure, les angles
 sont
des angles correspondants.
sont
des angles correspondants.
Deux angles correspondants sont tels que:
ils sont du même côté de
 .
.l'un est situé entre d et d', et l'autre à l'extérieur de d et d'
les deux ont l'un de leur côté situé sur
 ,
l'autre côté étant pour l'un sur d et pour
l'autre sur d'.
,
l'autre côté étant pour l'un sur d et pour
l'autre sur d'.
2.4.1.3. Angles alternes-externes (à titre culturel, hors-programme de 5e).
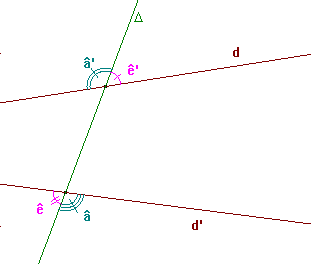
Sur la figure, les angles â et â' sont des angles alternes-externes, ainsi que les angles ê et ê'.
Deux angles alternes-externes sont tels que:
ils sont situés à l'extérieur de la bande de plan formée par les droites d et d'
ils sont de part et d'autres de
 .
.
2.4.2. Propriétés.
2.4.2.1. Propriétés directes.
Propriétés:
Soient deux droites d et d'
coupées par une sécante![]() .
.
Si les droites d et d' sont parallèles, alors deux angles alternes-internes sont de même mesure.
Si les droites d et d' sont parallèles, alors deux angles correspondants sont de même mesure.
Si les droites d et d' sont parallèles, alors deux angles alternes-externes sont de même mesure.
2.4.2.2. Propriétés réciproques.
Propriétés:
Soient deux droites d et d' coupées par une droite ![]() .
.
Si deux angles alternes-internes ont la même mesure, alors d et d' sont parallèles.
Si deux angles correspondants ont la même mesure, alors d et d' sont parallèles.
Si deux angles alternes-externes ont la même mesure, alors d et d' sont parallèles.