Sphères.
1. Sphère. Boule.
1.1. Définitions.
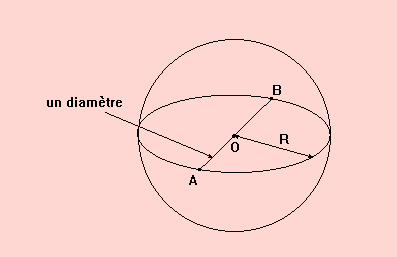
Définition: La sphère de centre O et de rayon R est l'ensemble des points de l'espace dont la distance à O est égale à R.
Définition: La boule de centre O et de rayon R est l'ensemble des points de l'espace dont la distance à O est inférieure ou égale à R. (C'est la sphère et son intérieur).
Définition: Toute droite passant par le centre d'une sphère coupe celle-ci en deux points diamétralement opposés.
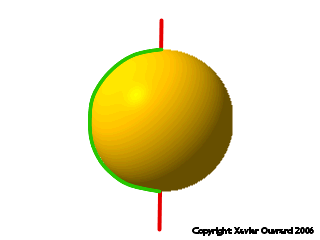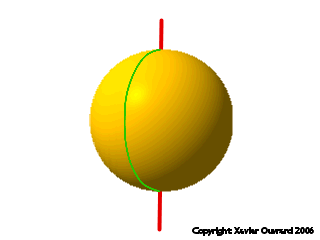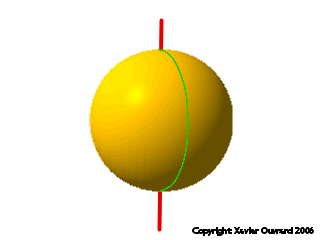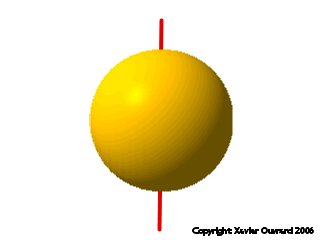
Une sphère est une surface de révolution: en effet, elle peut être engendrée par un demi-cercle, tournant autour d'un axe.
1.2. Aire et volume.
L'aire A d'une sphère de rayon R est:
Le volume V d'une boule de rayon R est:
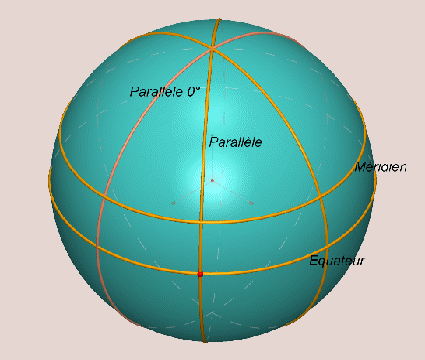
1.3. Repérage sur la terre.
2. Section d'une sphère par un plan.
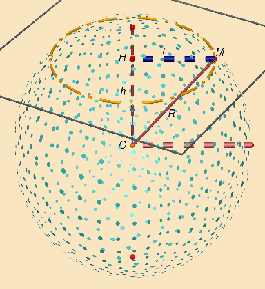
Théorème: Soit un plan P et une sphère de
centre O, de rayon R. Soit H le point du plan P tel que la droite
(OH) est perpendiculaire au plan P. Trois cas sont possibles:
1° cas: Si OH < R, alors le plan et la sphère se
coupent selon un cercle.
2° cas: Si OH = R, alors le plan et la sphère n'ont qu'un
seul point commun: on dit que le plan est tangent à la sphère.
3° cas: Si OH > R, alors le plan ne coupe pas la sphère.
Cas particulier: La section d'une sphère par un plan passant par le centre de la sphère est appelé grand cercle de la sphère: son rayon est celui de la sphère.
