Mesures de longueurs.
Polygones. Cercles. Disques.

Définition : Le segment qui a pour extrémités les points A et B se note [AB] ou [BA]. On note AB sa longueur.

Propriété : Deux segments ont même longueur lorsqu’ils sont superposables.

Unités de longueurs : L’unité légale de longueur est le mètre. On le note m.

On utilise également les multiples et les sous-multiples du mètre

Multiples du mètre			Mètre	Sous-multiples du mètre
km	hm	dam	m	dm	cm	mm

Définition : Le point I appartenant au segment [AB] tel que les segments [IA] et [IB] ont même longueur, est appelé le milieu du segment.

Définition : La médiatrice d’un segment est la droite :

• passant par le milieu du segment.

• et perpendiculaire à ce segment.

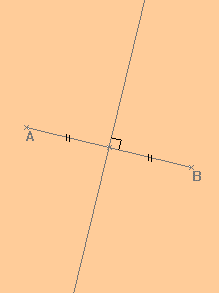
Propriété caractéristique de la médiatrice :
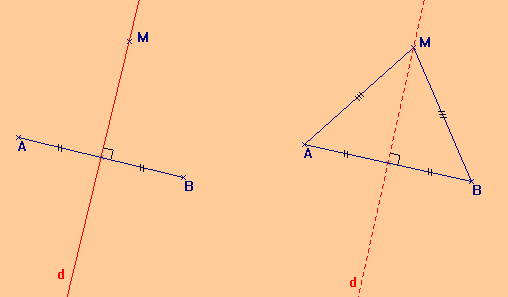
            1. Si un point est sur la médiatrice d’un segment, alors il est à égale distance des extrémités de ce segment.
            2. Si un point est à égale distance des deux extrémités d’un segment, alors il est sur la médiatrice de ce segment.

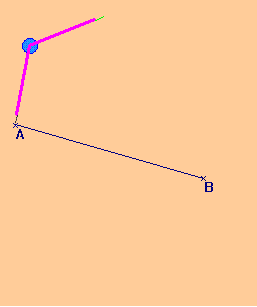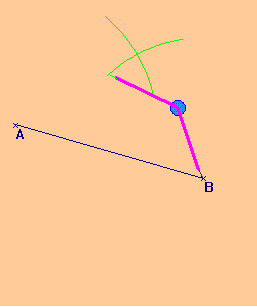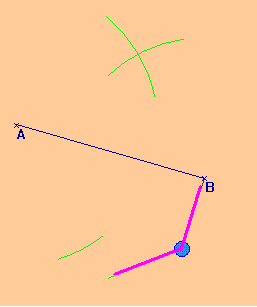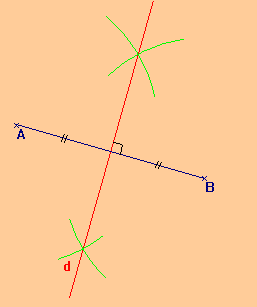
Construction au compas de la médiatrice :

Pour construire au compas et à la règle la médiatrice d’un segment, il suffit de construire deux points à égale distance des extrémités.

Définitions : On appelle ligne polygonale un ensemble de segments consécutifs.

Une ligne polygonale fermée est appelée un polygone. Dans ce cas les segments sont appelés côtés du polygone. Les extrémités des côtés sont appelés sommets.

Tout segment joignant deux sommets non consécutifs est appelé diagonale du polygone.

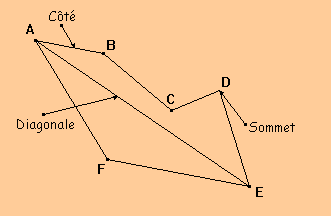
Exemple : Polygone ABCDEF :

Remarque : Le polygone ci-dessus Peut aussi s’appeler AFEDCB, ou encore BCDEFA, etc…

Nombre de côtés	Nom du polygone
3	Triangle
4	Quadrilatère
5	Pentagone
6	Hexagone
7	Heptagone
8	Octogone
10	Décagone
12	Dodécagone

Définition: Un triangle est un polygone ayant trois côtés.

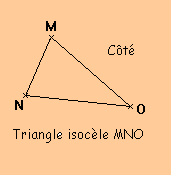
Définition : Un triangle isocèle est un triangle qui a deux côtés de même longueur.

Définition : Un triangle équilatéral est un triangle qui a trois côtés de même longueur.

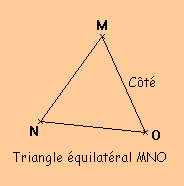
Définition : Un triangle rectangle est un triangle qui a un angle droit.

Définition : Un quadrilatère est un polygone qui a quatre côtés.

Définition : Un losange est un quadrilatère qui a quatre côtés de même longueur.

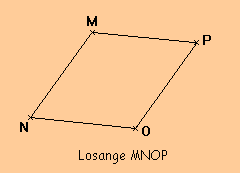
Définition : Un rectangle est un quadrilatère qui a ses côtés successifs perpendiculaires.

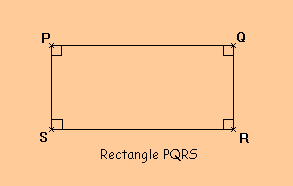
Remarque : Les côtés opposés d’un rectangle sont de même longueur et parallèles.

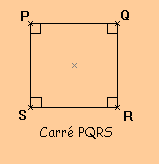
Définition : Un carré est à la fois un losange et un rectangle.

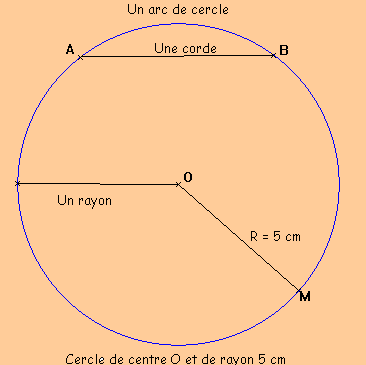
Définition : Le cercle de centre O, de rayon R est l’ensemble des points du plan situés à la distance R du point O. On le note C(O ;R).

signifie OM = R.

Exemple : R = 5 cm.

Règle : La longueur d’une ligne polygonale est la somme des longueurs des segments qui forment cette ligne.

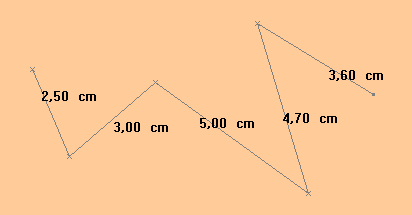
Exemple : Sur l’exemple ci-dessus :

2,5 + 3 + 5 + 4,7 + 3,6 = 18,8 cm.

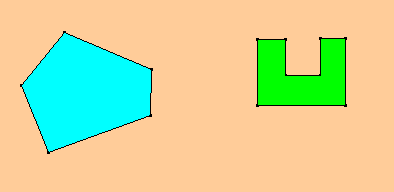
Définition : Le périmètre d’une surface est la longueur de la ligne qui délimite cette surface.

Exemple : Sur les figures ci-dessus, le périmètre de la surface coloriée est la longueur de la ligne noire.

Périmètre du triangle : Le périmètre du triangle est égale à la somme des longueurs de ses trois côtés.

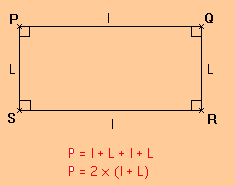
Périmètre du rectangle :

Périmètre du losange et du carré :

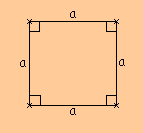
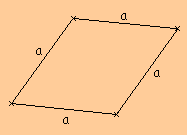
P = a + a + a + a

P = 4 x a

Périmètre du cercle :

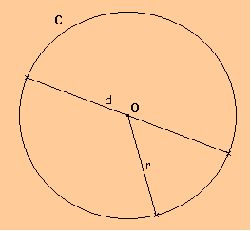
Le périmètre d’un disque de rayon r est égale à où (pi) est un nombre voisin de 3,14.

Exemple: La longueur d’un cercle de rayon 5 cm est cm = cm.

Remarque: Comme la longueur d’un diamètre d est égale à deux fois le rayon, on a la formule suivante:

.

Le nombre pi :

n’est pas un nombre décimal: il ne se termine jamais.

3,1 ; 3,14 ; 3,141 ; sont des approximations décimales du nombre .