|
Un cours de mathématiques du Collège au Lycée |
|
||
Triangles
1. Rappels. Construction de triangles.
1.1. Construction de triangles.
On connaît trois côtés:
ex. AB = 6 cm; BC = 3 cm et CA = 4 cm
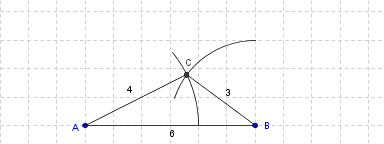
Exemple de construction d'un triangle connaissant trois longueurs Pour afficher la figure dynamique, cliquer ci-dessus.
On connaît deux côtés, un angle:
ex. AB = 6 cm ; BC = 3 cm et
Figure à venir
On connaît un côté et deux angles:
ex.1 AB = 6 cm;
et
Figure à venir
ex.2 AB = 5 cm;
et
Figure à venir
1.2. Inégalité triangulaire.
Propriété : Soit trois points A, B et M.
|
Si
AB = AM + MB |
Si
AB < AM + MB |
|
|
|
|---|
,
alors :
,
alors :
Utilité: Prévoir si un triangle est constructible.
Exemples:
On donne EF = 9 cm , FG = 6 cm et GE = 5 cm.
Comme, FG + GE = 11 cm et que 11>9 .
EF + FG = 15 cm et que 15 > 5
EF + GE = 14 cm et que 14>5
donc le triangle EFG est constructible.
Figure à venir
On donne EF = 9 cm, FG = 5 cm et GE = 4 cm
Comme, FG + GE = 5 + 4 = 9 cm, le point G appartient au segment [EF]
Figure à venir
On donne EF = 9 cm, FG = 5 cm et GE = 2 cm
Comme FG + GE = 7 cm < EF, le triangle EFG n'est pas constructible.
Figure à venir
Conséquence: Si deux droites sont perpendiculaires, alors leurs symétriques par rapport à un point sont perpendiculaires.
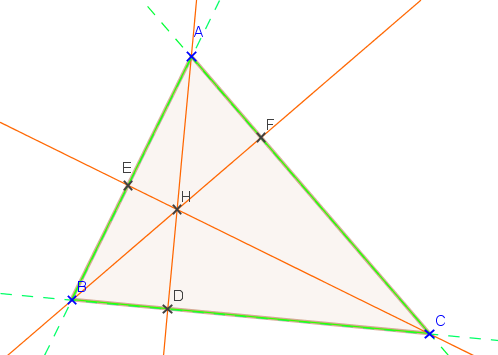
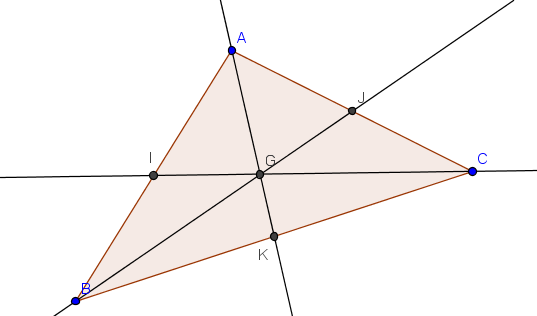
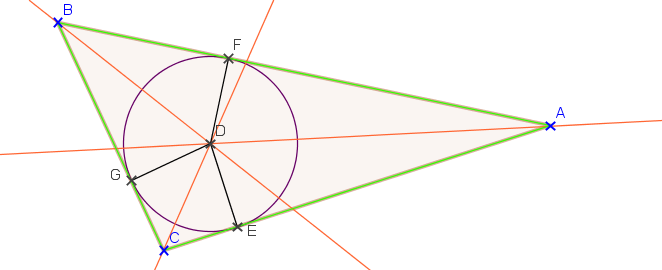
1.3. Droites remarquables du triangle.
Définition : Une hauteur d’un triangle est une droite passant par un sommet et perpendiculaire au côté opposé.
Pour afficher la figure dynamique, cliquer ci-dessus.
Définition : La médiatrice d’un segment est la droite qui passe par le milieu de ce segment et le coupe perpendiculairement.
Pour afficher la figure dynamique, cliquer ci-dessus.
Définition : Une médiane d’un triangle est une droite passant par un sommet et reliant le milieu du côté opposé.
Pour afficher la figure dynamique, cliquer ci-dessus.
Définition : La bissectrice d’un angle est la droite qui partage cet angle en deux angles égaux.
Pour afficher la figure dynamique, cliquer ci-dessus.
2. Quelques propriétés du triangle.
2.1. Somme des mesures d'un angle.
Propriété: La somme des mesures des angles d'un triangle est égale à 180°.
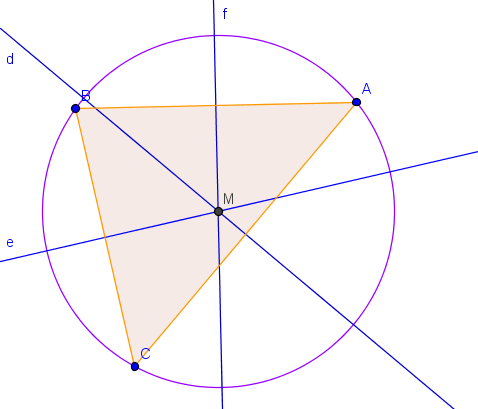
2.2. Exemple de construction des médiatrices d'un triangle.
Propriété (admise): Les médiatrices d'un triangle sont concourantes. Le point de concours des médiatrices d'un triangle est le centre d'un cercle passant par ses trois sommets. Ce cercle s'appelle le cercle circonscrit au triangle.
Figure à venir
2.3. Aire d'un triangle..
Propriété:
On a:
,
où:
b: longueur de la base (d'un côté)
h: longueur de la hauteur issue du sommet non extrémité de la base.
3. Triangles particuliers.
3.1. Triangle rectangle.
Définition: Un triangle est rectangle si il a un angle droit. Le côté opposé à l'angle droit est appelé l'hypoténuse.
Propriété: La somme des mesures des deux angles aigus non droits est égale à 90°.
Propriété: Le milieu de l'hypoténuse d'un triangle rectangle est le centre de son cercle circonscrit.
3.2. Triangle isocèle.
Définition: Un triangle est isocèle si il a deux côtés de même longueur. Le sommet commun aux deux côtés de même longueur est appelé sommet principal.
Propriété: Dans un triangle isocèle, la hauteur issue du sommet principal est également la médiane issue de ce sommet, la médiatrice du côté opposé et la bissectrice du sommet principal. Cette droite est le seul axe de symétrie d'un tel triangle.
Propriété: Les angles à la base d'un triangle isocèle sont de même mesure.
3.3. Triangle équilatéral.
Définition: Un triangle est équilatéral si tous ses côtés sont de même longueur.
Propriété: Dans un triangle équilatéral, les hauteurs sont aussi les médianes, les bissectrices et les médiatrices du triangle. Ce sont également les axes de symétrie de ce triangle. Leur point de concours est le centre de symétrie de ce triangle.
Propriété: Dans un triangle équilatéral, tous les angles ont la même mesure, à savoir 60°.