Triangle rectangle et cercle circonscrit.

Définition : La médiatrice d’un segment est la droite qui passe par le milieu de ce segment et le coupe perpendiculairement.

Propriété caractéristique de la médiatrice:
1. Si un point est sur la médiatrice d’un segment alors il est équidistant des extrémités de ce segment.
2. Réciproquement, si un point est équidistant des extrémités d’un segment, alors ce point est sur la médiatrice de ce segment.

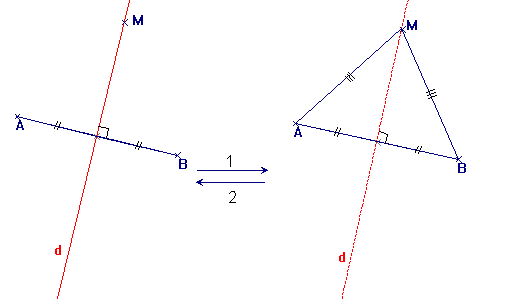
M est sur la médiatrice d de [AB]	M est équidistant de A et de B

Pour des rappels plus détaillés sur la médiatrice: voir ici

Théorème : Les médiatrices des côtés d’un triangle non aplati sont concourantes en un point qui est le centre du cercle circonscrit à ce triangle.

Les médiatrices d'un triangle: Pour afficher la figure dynamique, cliquer sur la figure.

Remarque : 1. Pour obtenir le centre du cercle circonscrit, il suffit de tracer les médiatrices de deux côtés ; en traçant la troisième, on peut ainsi vérifier que l’on ne s’est pas trompé !
2. Le centre du cercle circonscrit est à égale distance des sommets du triangle.

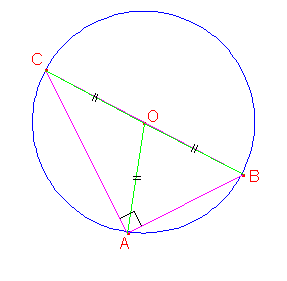
Théorème direct : Si un triangle est rectangle, alors son hypoténuse est un diamètre de son cercle circonscrit.

Remarques : Dans un triangle rectangle :

- le milieu de l’hypoténuse est le centre du cercle circonscrit au triangle.

- la longueur du segment qui joint le sommet de l’angle droit au milieu de l’hypoténuse est la moitié de la longueur de l’hypoténuse.

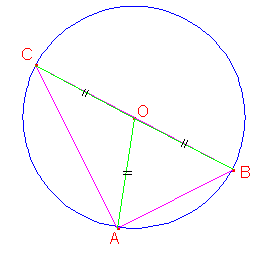
Théorème réciproque : Si l’un des côtés d’un triangle est un diamètre de son cercle circonscrit, alors ce triangle est rectangle (le diamètre du cercle circonscrit est alors son hypoténuse).

Remarques : M étant le milieu du côté [BC] d’un triangle ABC, si , alors le triangle est rectangle en A.