Sections. Agrandissement Réduction.

Propriété: La section d'un parallélépipède rectangle par un plan parallèle à une face est un rectangle superposable à cette face.

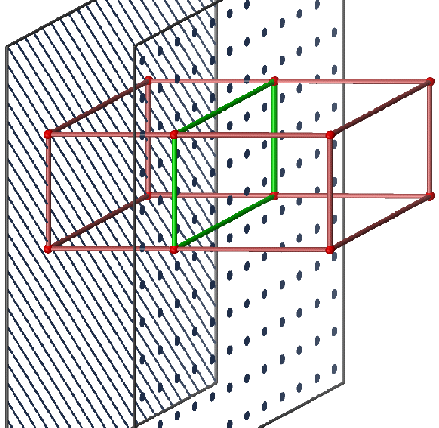
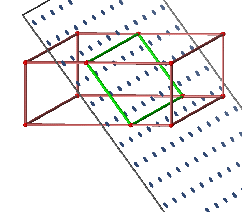
Propriété: La section d'un parallélépipède rectangle par un plan parallèle à une arête est un rectangle dont une dimension est la longueur de cette arête.

Propriété: La section d'un cylindre de révolution par un plan perpendiculaire à son axe est un disque superposable aux disques de base.

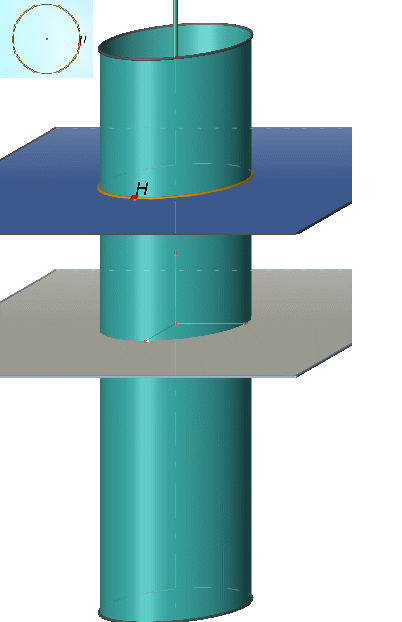
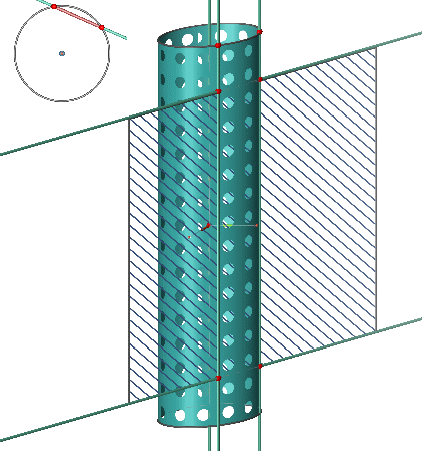
Propriété: La section d'un cylindre de révolution par un plan parallèle à son axe est un rectangle dont une dimension est la hauteur du cylindre.

Si on agrandit ou si on réduit une figure, cela signifie que dans cette figure :

• Les angles sont conservés.

• Les dimensions sont multipliées par un même nombre, soit k.

Si k>1, il s’agit d’un agrandissement.

Si k<1, il s’agit d’une réduction.

Si les longueurs sont multipliées par k, alors :

• le périmètre est aussi multiplié par k.

• les aires sont multipliées par k².

• les volumes (si on est dans l’espace) sont multipliés par k³.

La section d’une pyramide ou d’un cône de révolution par un plan parallèle à sa base est une réduction de cette base.

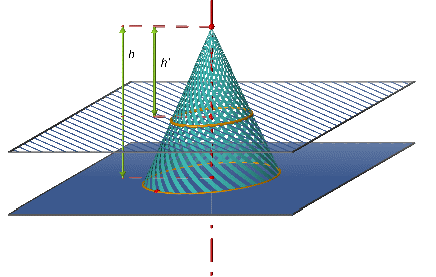
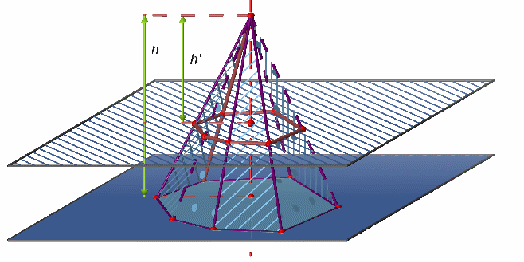
L’échelle de réduction est .