Parallélogramme et translation.

Définition : Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.

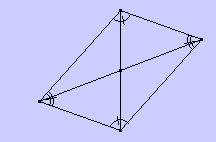
Propriétés : Un parallélogramme a un centre de symétrie : le point d’intersection de ses diagonales. Dans un parallélogramme, on a alors les propriétés suivantes :
- les diagonales se coupent en leur milieu ;
- les côtés opposés ont la même longueur ;
- les angles opposés ont la même longueur ;
- deux angles consécutifs sont supplémentaires.

Propriétés caractéristiques :
1. Si les côtés opposés d’un quadrilatère sont parallèles, alors ce quadrilatère est un parallélogramme.
2. Si les diagonales d’un quadrilatère se coupent en leur milieu, alors ce quadrilatère est un parallélogramme.
3. Si les côtés opposés d’un quadrilatère non croisé ont même longueur, alors ce quadrilatère est un parallélogramme.

2. Translation.

Découverte de la translation:

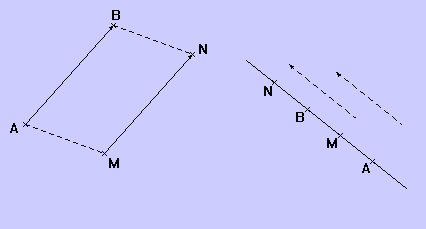
Définition : Soit deux points A et B et un point M. L’image du point M par la translation qui transforme A en B est le point N tel que ABNM soit un parallélogramme (éventuellement aplati si A, B et M sont alignés).

Propriétés :
- L’image par une translation d’un segment est un segment de même longueur et parallèle.
- L’image par une translation d’une droite est une droite parallèle (éventuellement confondue).
- L’image par une translation d’une demi-droite est une demi-droite parallèle.
- L’image par une translation d’un cercle est un cercle de même rayon.

Propriétés : Par une translation, on conserve les distances, l’alignement, les angles et les aires.