Puissances. Notation scientifique.

Définition : Soit a un nombre quelconque, on écrit pour tout entier n supérieur à 1 :

Par convention, pour a non nul, a⁰ = 1.

En clair, le produit de n facteurs égaux à a est noté aⁿ, et on lit « a puissance n ». aⁿ est appelé une puissance du nombre a. Le nombre n est appelé exposant.

Exemple :  ;

 ;

A ne pas confondre avec :  ;

.

Remarques importantes :

• Dès que a est non nul, l’inverse de aⁿ existe et vaut 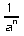. On le notera a^-n. On peut donc considérer que l’écriture aⁿ est valable pour tout entier relatif n, dès que a est non nul.

• Attention ! L’écriture 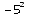désigne l’opposé du carré de 5 et non le carré de –5. Le carré de –5 s’écrit : 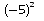. Il ne faut pas oublier les parenthèses lorsque l’on prend la puissance d’un nombre négatif.

• La puissance paire d’un nombre négatif est toujours positive.

• La puissance impaire d’un nombre négatif est toujours négative.

Propriétés : Soit a et b deux nombres non nuls.
Pour tous les nombres relatifs m, n :

Exemples :

Remarque : Attention ! Il n’existe aucune formule avec l’addition :

n’est pas égal à , mais à .

n’est pas égal à , mais à .

Remarque : Pour tout entier n supérieur à 1, on écrit :

Par convention 10⁰ = 1.

Exemples : Voici quelques valeurs de puissances de 10 portées dans le tableau suivant :

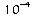
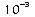
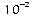
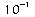
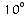
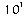
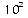
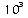
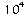
0,0001	0,001	0,01	0,1	1	10	100	1000	10000

Remarque : et sont des nombres inverses. On peut donc considérer que l’écriture est valable pour tout entier relatif n.

Propriétés : Pour tous les nombres relatifs m, n :

Exemples :

Définition : La notation scientifique d’un nombre décimal non nul est son écriture de la forme , où a est un décimal qui a un seul chiffre non nul avant la virgule.

Exemples :  ;

.

Remarque : On détermine un ordre de grandeur d’un nombre en le plaçant entre deux puissances de dix consécutives. On choisit alors la plus proche du nombre, comme ordre de grandeur.

Exemples : a pour ordre de grandeur  ;

a pour ordre de grandeur .

Remarque : Il existe d’autres notations d’un décimal utilisant les puissances de 10, en particulier la notation ingénieur.