De la translation aux vecteurs.

Définition: Lorsque deux droites sont parallèles, on dit qu'elles ont la même direction. Une direction étant donnée, on peut choisir sur celle-ci un sens.

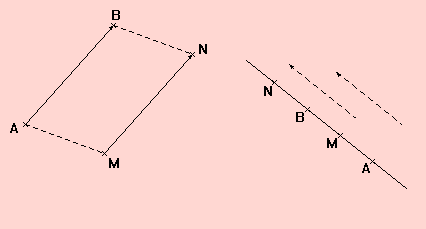
Définition : On se donne deux points A et B fixés et un troisième point M. L’image du point M par la translation qui transforme A en B est le point N tel que ABNM soit un parallélogramme (éventuellement aplati si A, B et M sont alignés.

Propriétés :
L’image par une translation d’un segment est un segment de même longueur et parallèle.
L’image par une translation d’une droite est une droite parallèle (éventuellement confondue).
L’image par une translation d’une demi-droite est une demi-droite parallèle.
L’image par une translation d’un cercle est un cercle de même rayon.

Propriétés : Par une translation, on conserve les distances, l’alignement, les angles et les aires.

Définition : La donnée d’une direction, d’un sens sur cette direction et d’une longueur définit un vecteur.

Notation : Soit deux points A et B. On notele vecteur définit par la direction de la droite (AB), le sens allant de A vers B et la longueur étant celle du segment [AB].

Définition: Deux vecteurs qui ont même direction, même sens et même longueur sont dits égaux.

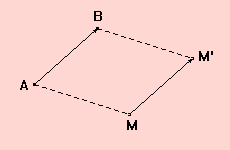
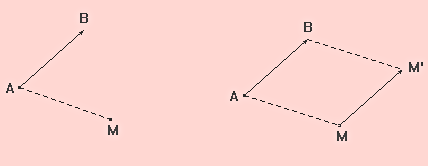
Soit A et B deux points. L’image de M par la translation qui transforme de A en B est le point M’ tel que : MM’ = AB et les demi-droites [AB) et [MM’) soient parallèles et de même sens. Ce qui revient à dire que ABM’M est un parallélogramme, ou encore que .

Propriété : Soit quatre points non alignés A, B, C et D.
Si alors ABDC est un parallélogramme.
Réciproquement, si ABDC est un parallélogramme, alors :

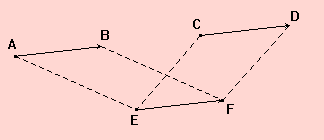
Remarque : Si A, B, C, et D sont alignés. Soit E et F les points tels que ABFE et CDFE soient des parallélogrammes.

.

Propriété : Appliquer une translation de vecteur suivie d'une translation de vecteur revient à appliquer une translation de vecteur .

Propriété de Chasles : (mathématicien français (1793 – 1880))
Pour tous points A, B et C, on a : .

Remarque : . On pose :

Propriété : (dite règle du parallélogramme)
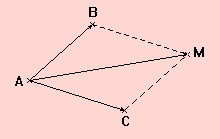
Soit A, B et C trois points. Soit M un point tel que ABMC soit un parallélogramme. Alors : .
Réciproquement, si M est un point tel que: , les points A, B et C étant donnés, alors ABMC est un parallélogramme.

Propriété :L’action successive sur une figure d’une symétrie de centre I, suivie d’une symétrie de centre J, est identique à l’action de la translation de vecteur.