Equations et inéquations.
1. Equations.
1.1 Définitions. Vocabulaire.
Définition: On appelle équation une égalité entre deux expressions algébriques.
Exemple:
![]() ,
,
![]() ,
,
![]() sont
des équations. La première comporte une seule inconnue,
x. La deuxième comporte deux inconnues x et y. La troisième
comporte à nouveau une seule inconnue, x. Cette dernière
est élevée au carré, on dit donc de la troisième
équation que c'est une équation du second degré.
Les deux premières équations sont du premier degré.
sont
des équations. La première comporte une seule inconnue,
x. La deuxième comporte deux inconnues x et y. La troisième
comporte à nouveau une seule inconnue, x. Cette dernière
est élevée au carré, on dit donc de la troisième
équation que c'est une équation du second degré.
Les deux premières équations sont du premier degré.
Vocabulaire: Dans une équation, on distingue les membres de cette équation, c'est à dire les expressions algébriques qui sont de part et d'autres du signe égal. Une équation comporte donc deux membres: le premier et le deuxième, ou encore le membre de gauche et le membre de droite.
Définitions : Résoudre une équation, c’est trouver toutes les valeurs que l’on peu donner à l’inconnue pour que l’égalité soit vraie. Ces valeurs sont les solutions de l’équation.
Dans un premier temps, nous allons nous intéresser uniquement aux équations à une seule inconnue du premier degré, ou à celles qui peuvent s'y ramener.
Tout d'abord revoyons deux équations de référence vues dans les classes antérieures.
1.2. Equations de références a + x = b ; ax = b.
1.2.1. a + x = b.
Propriété: L’équation a + x = b d’inconnue x a pour solution x = b – a.
Exemple :
![]()
La solution de l’équation 3 + x = -7 est –10.
1.2.2. ax = b.
Propriété:
L’équation ax = b d’inconnue x:
-
Si
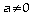 ,
admet une seule solution x = b/a.
,
admet une seule solution x = b/a. -
Si
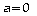 et
si
et
si
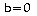 ,
une infinité de solution.
,
une infinité de solution. -
Si
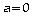 et
si
et
si
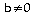 ,
aucune solution.
,
aucune solution.
En pratique, en classe de Troisième, on ne s'intéressera qu'au premier cas.
Exemple :
![]()
L'équation -4x = 7
admet une seule solution:
![]() .
.
1.3. Méthode de résolution d'une équation à une inconnue du premier degré.
L’objectif est de ramener l’équation à une équation de référence du § 1.2.
Pour cela on dispose des deux règles suivantes :
Règle 1 : On ne change pas les solutions d’une équation en ajoutant ou en retranchant un même nombre aux deux membres de l’équation.
Règle 2 : On ne change pas les solutions d’une équation en multipliant ou en divisant par un même nombre non nul les deux membres de l’équation.
Exemple : Résoudre l’équation :
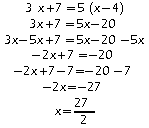
L'équation
![]() admet
une seule solution:
admet
une seule solution:
![]() .
.
Savoir : Mettre en équation un problème
Méthode:
Pour mettre en équation
un problème, on respectera les étapes suivantes:
1. Choix de l'inconnue.
2. Mise en équation du
problème.
3. Résolution de
l'équation.
4. Conclusion, en vérifiant
si la (ou les) solution(s) répondent au problème posé.
1.4. Equation-produit.
1.4.1. Nullité d’un produit.
Propriétés :
1. Si l’un des facteurs
d’un produit est nul, alors ce produit est nul.
2. Réciproquement, si
un produit est nul, alors l’un au moins de ses facteurs est
nul.
1.4.2. Définition et méthode de résolution d’une équation-produit.
Définition: Une équation-produit est une équation à une inconnue où le premier est un produit de facteurs du premier degré (chaque facteur est du type ax + b, où a et b sont deux nombres) et dont le second membre est nul.
Exemple : (4x – 3) (x + 7) = 0
Remarque: Les équations-produit sont le premier type d'équation à une inconnue de degré supérieur strictement à 1 vu dans la scolarité au collège. En pratique, on se limite à deux ou trois facteurs, c'est à dire à des équations du second ou troisième degré.
Méthode de résolution :
On désigne par A = 4x – 3 et B = x + 7.
Règle : A
et B désignant deux expressions du premier degré de la
même variable :
Si AB = 0, alors A = 0 ou B
= 0.
Sur l’exemple :
(4x – 3)(x + 7) = 0 alors 4x – 3 = 0 ou x + 7 = 0
x = ¾ ou x = -7.
Les solutions de (4x –
3)(x + 7) = 0 sont –7 et
![]() .
.
Savoir: Factoriser pour résoudre une équation.
Afin de se ramener à une équation produit, il est parfois nécessaire de commencer par factoriser l'équation donnée. Pour cela, on dispose de toutes les formules vues dans le paragraphe sur la factorisation, du chapitre Développement. Identités remarquables. Factorisation.
2. Inéquations à une inconnue du premier degré.
2.1. Ordre et opérations.
2.1.1. Comparaison de deux nombres relatifs.
Règles :
1. Si deux nombres sont de signes différents, le plus petit
est le nombre négatif.
2. Si deux nombres sont
négatifs, on les range dans l’ordre inverse de leurs
opposés.
Exemple : Ranger par ordre croissant : -4,53 ; +4,5 ; -4,503.
-4,53 < -4,503 < +4,5.
2.1.2. Ordre et addition.
Règle : 3. L’ordre est conservé lorsque l’on ajoute un même nombre aux deux membres d’une inégalité.
Exemples : 1.
Comparer :
![]() et
et
![]() .
.
Comme :
![]() ,
on a : a < b.
,
on a : a < b.
2. Si x vérifie x + 7 < 3,5, alors on a : x + 7 + (-7) < 3,5 + (-7) d'où: x < -3,5.
2.1.3. Ordre et multiplication.
Règles :
4. L’ordre est conservé quand on multiplie les deux
membres d’une inégalité par un même nombre
strictement positif.
5. L’ordre est inversé
quand on multiplie les deux membres d’une inégalité
par un même nombre strictement négatif.
Exemples : 1. Si x vérifie :
![]() alors on a, puisque
alors on a, puisque
![]() :
:
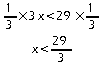
2. Si x vérifie :
![]() ,
alors, on a, puisque
,
alors, on a, puisque
![]() :
:
![]()
2.2. Inéquations du premier degré à une inconnue.
2.2.1. Généralités
Définition: On appelle inéquation une inégalité entre deux expressions algébriques.
Exemple:
![]() ,
,
![]() ,
,
![]() sont
des inéquations. La première comporte une seule
inconnue, x. La deuxième comporte deux inconnues x et y. La
troisième comporte à nouveau une seule inconnue, x.
Cette dernière est élevée au carré, on
dit donc de la troisième équation que c'est une
inéquation du second degré. Les deux premières
inéquations sont du premier degré.
sont
des inéquations. La première comporte une seule
inconnue, x. La deuxième comporte deux inconnues x et y. La
troisième comporte à nouveau une seule inconnue, x.
Cette dernière est élevée au carré, on
dit donc de la troisième équation que c'est une
inéquation du second degré. Les deux premières
inéquations sont du premier degré.
Vocabulaire: Dans une inéquation, on distingue les membres de cette inéquation, c'est à dire les expressions algébriques qui sont de part et d'autres du signe d'ordre. Une inéquation comporte donc deux membres: le premier et le deuxième, ou encore le membre de gauche et le membre de droite.
Définitions : Résoudre une inéquation, c’est trouver toutes les valeurs que l’on peu donner à l’inconnue pour que l’inégalité soit vraie. Ces valeurs sont les solutions de l’inéquation.
En classe de Troisième, nous nous intéresserons uniquement aux inéquations à une seule inconnue du premier degré, ou à celles qui peuvent s'y ramener.
2.2.2. Méthode de résolution
Méthode de résolution : Comme pour les équations, on isole les x en utilisant les règles rappelées en 2.1., qui ne changent pas les solutions de l'inéquation.
Exemple: Résoudre l'inéquation suivante:
![]()
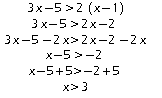
Les solutions de l’inéquation 3x – 5 > 2(x – 1) sont représentées graphiquement par :

Savoir : Mettre un problème en inéquation.
Méthode:
Pour mettre en équation
un problème, on respectera les étapes suivantes:
1. Choix de l'inconnue.
2. Mise en équation
du problème.
3. Résolution de
l'équation.
4. Conclusion, en vérifiant
si la (ou les) solution(s) répondent au problème posé.
