|
Un cours de mathématiques du Collège au Lycée |
|
||
Fractions
1. Préliminaires.
1.1.Définition.
Notation :
Le quotient du nombre a par le nombre non nul b s’écrit sous forme fractionnaire :
(a
est le numérateur, b est le dénominateur).
Exemple :
est
une écriture fractionnaire du quotient de 8,4 par 2, donc
Définition :
Lorsque a est entier relatif et b est un
entier relatif non nul,
est
une fraction.
Exemple :
sont
des fractions ; mais
n’est pas une fraction.
1.2. Règle fondamentale.
Règle : On ne change pas un nombre relatif en écriture fractionnaire en divisant (ou en multipliant) son numérateur et son dénominateur par un même nombre non nul.
Remarque :
Cela permet d’obtenir différentes écritures
fractionnaires d’un même nombre.
|
|||
|
Exemple :
|
|||
S'entraîner à la simplification de fractions
2. Addition. Soustraction.
2.1. Addition.
Règle :
Pour additionner deux nombres relatifs en écriture
fractionnaire, il faut :
1. S’assurer qu‘elles
ont le même dénominateur, sinon il faut les réduire
au même dénominateur ;
2. Additionner les
numérateurs ;
3. Conserver le dénominateur
commun.
|
|||
|
Exemple :
|
|||
2.2. Soustraction.
2.2.1. Nombres opposés.
Exemples :
L’opposé de
est :
ou
ou
.
L’opposé de
est :
ou
.
Remarque : La
somme de deux nombres opposés est égale à zéro.
2.2.2. Soustraction.
Règle :
Pour soustraire un nombre relatif à un autre, il faut ajouter
son opposé.
Exemple :
3. Multiplication.
Règle :
Pour multiplier deux nombres relatifs en écriture
fractionnaire, on multiplie les numérateurs entre eux et les
dénominateurs entre eux, tout en respectant la règle
des signes.
|
|||
|
Exemple : |
|||
S'entraîner à la multiplication de fractions relatives (niveau 1)
S'entraîner à la multiplication de fractions relatives (niveau 2)
S'entraîner à la multiplication de fractions relatives (niveau 3)
4. Division.
4.1. Inverse d’une fraction.
Règle : Deux nombres relatifs sont dits inverses lorsque leur produit est égal à 1.
Tout nombre relatif non nul
a admet un inverse noté
ou
a-1.
Exemples :
L’inverse de (-8) est
car
L’inverse de
est
car
.
Remarque : Si a
et b sont deux nombres non nuls, l’inverse de
est
.
4.2. Division.
Règle :.Diviser par un nombre relatif (non nul), c’est multiplier par son inverse .
Exemples :
S'entraîner à la division de fractions relatives (niveau 1)
S'entraîner à la division de fractions relatives (niveau 2)
Conséquence:
Soient a, b, c et d quatre nombres, avec b, c et d non nuls. On a
donc:
.
Remarque:
L'inverse de
est
,
pour c et d non nuls. En résumé, avec les notations
précédentes:
.
Conséquence: Ecriture étagée d'un quotient de fractions.
Soient a, b, c et d quatre
nombres, avec b, c et d non nuls. Le quotient de
par
,
noté jusqu'à présent:
,
peut se noter en écriture fractionnaire:
et
l'on a donc:
.
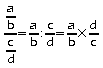Il faudra donc faire attention à la place du signe = !
S'entraîner à la division de fractions relatives étagées (niveau 1)
S'entraîner à la division de fractions relatives étagées (niveau 2)