|
Un cours de mathématiques du Collège au Lycée |
|
||
Angles, rotations, polygones réguliers.
1. Angles inscrits dans un cercle.
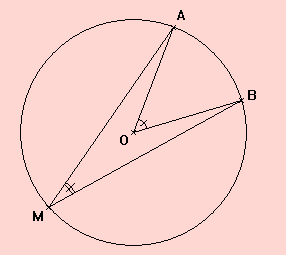
Définitions : 1. L’angle
est
appelé angle au centre qui intercepte le petit arc
2.
est
appelé angle inscrit interceptant le petit arc
Remarque : L’angle au centre et l’angle
inscrit interceptent le même arc.
Théorème de l’angle inscrit :
Dans un cercle, un angle inscrit est égal à la moitié de l’angle au centre interceptant le même arc.
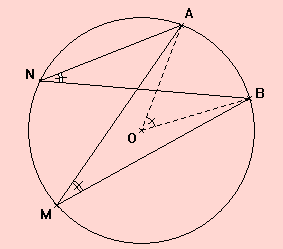
Angles inscrits interceptant le même arc :
Deux angles inscrits interceptant le même arc sont égaux.
.2. Rotation.
-
Définition :
Soit un point O et
un angle
.M’ image de M, distinct de O, par la rotation de sens direct, de centre O et d’angle
,
est le point tel que :OM’ = OM
Le sens pour aller de M à M’ est celui du sens direct.
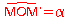
L'image de O est O.
Remarques:Le sens direct en mathématiques est celui qui est inverse aux aiguilles d’une montre (classique !)
La symétrie centrale n'est qu'un cas particulier de rotation avec un angle de 180°.
Une rotation d'angle 90° est appelé un quart de tour.
Propriétés : 1. La rotation conserve l’alignement, les distances, les angles et les aires.
2. Par une rotation, l’image :
d’un segment est un segment de même longueur ;
d’une droite est une droite ;
d’un cercle est un cercle de même rayon.
3. Polygones réguliers.
Exemples
de construction d'un polygone régulier connaissant son centre
et un sommet:
Triangle équilatéral:
Carré:
Hexagone régulier:
