Ordre et opérations. Valeurs approchées.
1. Comparaison de nombres relatifs.
1.1. Comparaison de deux nombres positifs (rappel de 5°).
Règle 1: Pour
comparer deux nombres positifs en écriture décimale, on
compare successivement les décimales de même rang.
Exemple: m = 61 ,
32564998 n = 61,32571 donc m < n.
Règle 2: Pour
comparer deux nombres positifs en écriture fractionnaire, il
faut d'abord les réduire au même dénominateur,
puis les ranger dans l'ordre de leur numérateur.
Exemple: 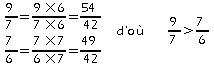
1.2. Comparaison de deux nombres relatifs.
Règle 3: Pour
comparer deux nombres relatifs, on distingue trois cas:
1er cas:
Si les deux nombres sont positifs, on utilise les règles 1 et
2 ou d'autres (cf Savoir)
2e cas:
Si les deux nombres sont de signes contraires, le plus petit est le
nombre négatif.
3e cas:
Si les deux nombres sont négatifs, ils sont rangés
dans l'ordre inverse de leurs opposés.
Exemple: m = - 61 , 32564998 n = - 61,32571 donc m > n.
m = 3/4 n = - 4/5 donc
n < m.
Règle 4:
Comparer deux nombres relatifs, revient à étudier le
signe de leur différence:
- dire que a - b < 0
revient à dire que a < b.
- dire que a - b > 0
revient à dire que a > b.
Savoir: Autres méthodes de comparaison
Règle de
transitivité: Si![]() et
et
![]() alors
alors
![]() .
.
Comparaison de fractions de même
numérateur: Elles sont classées dans l'ordre inverse de leur dénominateur.
2. Ordre et opération.
2.1. Ordre et addition.
Règle 5: Soit
trois nombres a, b, et c. Les nombres a + c et b + c sont rangés
dans le même ordre que les nombres a et b.
Exemple: M = -23 +
27,1 et N = -19 + 27,1. On a: -23 < -19 d'où M < N.
2.2. Ordre et multiplication.
Règle 6: Soit
trois nombres a, b, et k. Les nombres ka et kb sont rangés:
si k est strictement
positif, dans le même ordre que les nombres a et b.
Exemple:
![]() et
et
![]() .
On a: 6,9 < 7,8 d'où M > N.
.
On a: 6,9 < 7,8 d'où M > N.
Remarque: Si k est
strictement négatif, les nombres ka et kb sont rangés
dans l'ordre inverse des nombres a et b.
Exemple:
![]() et
et
![]() .
On a: 1,2 < 2,7 d'où M < N.
.
On a: 1,2 < 2,7 d'où M < N.
3. Encadrements. Valeurs approchées.
Remarque:
Il faut faire très attention dans la manipulation des
encadrements. Ainsi, si on veut montrer qu'un nombre x est compris
entre deux nombres a et b, il est plus simple de montrer que x est
plus grand que a et que x est plus petit que b. On peut alors
utiliser toutes les règles vues ci-dessus, ainsi que la règle
de transitivité.
Remarque: Il faut bien distinguer valeur approchée et troncature.
Pour une troncature, on coupe le nombre à la précision voulue, sans s'occuper du morceau à droite de la coupure.
Pour une valeur approchée,
on coupe le nombre à la précision voulue et on regarde
le morceau de droite: si il commence par 0, 1, 2, 3 ou 4, l'arrondi
est égal à la troncature. Sinon l'arrondi est égal
à la troncature + la précision.
Exemple: Soit m=67,9457
La troncature au dixième de m est 67,9. L'arrondi au dixième de m est aussi 67,9.
La troncature au centième de m est 67,94. L'arrondi au centième de m est 67,95.
