Triangle : milieux et parallèles.

Propriétés : Si deux droites parallèles sont coupées par une sécante, alors :
                        1. deux angles alternes-internes sont égaux.
                        2. deux angles correspondants sont égaux.
Réciproquement :
                        1. Si deux droites sont coupées par une sécante en formant deux angles en configuration d’angles alternes-internes qui sont égaux, alors elles sont parallèles et les deux angles sont alternes-internes.
                        2. Si deux droites sont coupées par une sécante en formant deux angles en configuration d’angles correspondants qui sont égaux, alors elles sont parallèles et les deux angles sont correspondants.

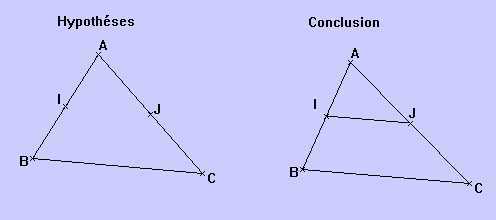
Théorème direct des milieux : Dans un triangle, si une droite passe par les milieux de deux côtés, alors elle est parallèle au troisième côté, et de plus la longueur du segment joignant les deux milieux est égale à la moitié de la longueur du troisième côté.

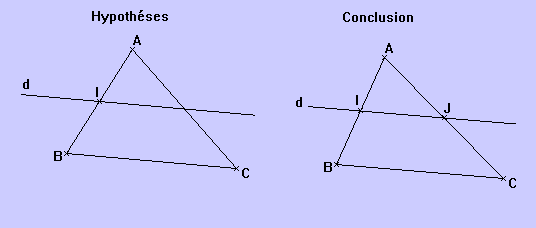
Théorème réciproque des milieux : Dans un triangle, si une droite passe par le milieu d’un côté, et si elle est parallèle à un second côté, alors elle coupe le troisième en son milieu.

Règle (dite du produit en croix) : Soit a, b, c et d quatre nombres non nuls.
                    Si alors ad = bc.

Conséquences : 1. Alors : .

2. Si , on a aussi . C’est à dire que deux quotients égaux, ont des inverses égaux.

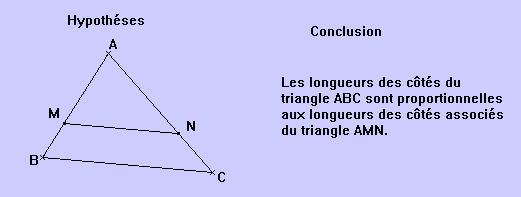
Théorème (partiel) de Thales : Dans un triangle ABC, si M est un point du côté [AB], N un point du côté [AC] et si (MN) est parallèle à (BC), alors :
                                                           

Remarque : Les côtés de même support ou de supports parallèles sont appelés côtés associés.

Remarque:sont des côtés associés.

Remarque : Le théorème réciproque des milieux n’est qu’un cas particulier de ce théorème.