|
Un cours de mathématiques du Collée au Lycée |
|
||
Du côté des angles.
1. Cosinus, sinus et tangente d’un angle aigu.
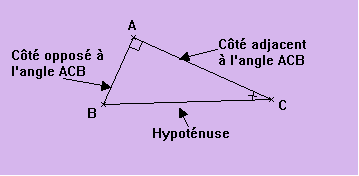
1.1.Définitions.
Définition :
Soit un triangle ABC, rectangle en A. On pose :
.
Définition :
Soit un triangle ABC, rectangle en A. On pose :
.
Remarque : Le
cosinus et le sinus d’un angle aigu sont compris entre 0 et 1.
1.2. A la calculatrice.
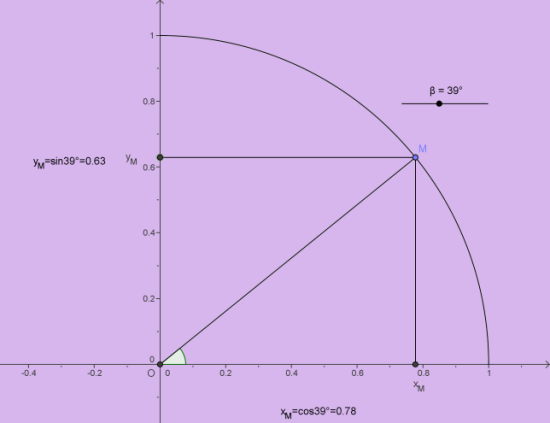
Valeurs du cosinus et du sinus d'un angle aigu: Pour afficher la figure dynamique, cliquer ci-dessus.
Remarques : - Ne pas oublier de mettre la calculatrice en degrés.
- Calcul de l’angle  tel que : sin  = 0,75.
Appuyer sur sin-1
ou inv sin
Remarques : - Ne pas oublier de mettre la calculatrice en degrés.
- Calcul de l’angle  tel que : tan  = 4.
Appuyer sur tan-1 ou inv tan
2. Relations entre sinus, cosinus et tangente.
2.1. Relations entre sinus et cosinus.
2.1.1. Angles complémentaires.
Propriété :
Lorsque deux angles sont complémentaires, le sinus de l’un
est égal au cosinus de l’autre.
2.1.2. Propriétés des carrés.
Propriété :
Quelque soit l’angle aigu
:
2.2. Relation entre cosinus, sinus et tangente.
Propriété :
Quelque soit l’angle aigu
,
différent de 90° :
3. Valeurs remarquables de sinus et de cosinus.
|
|
0 |
30 |
45 |
60 |
90 |
|
|
0 |
|
|
|
1 |
|
|
1 |
|
|
|
0 |
|
|
0 |
|
1 |
|
XXX |
