De la symétrie centrale

Pour commencer, on observe la figure ci-dessous:

Définitions. Vocabulaire:

On se donne deux points O et A.

1. On dit que A' est le symétrique de A par rapport au point O, si O est le milieu de [AA'].

2. Dans ce cas, on peut aussi dire que A et A' sont symétriques par rapport au point O.

3. Une symétrie par rapport à un point est appelée symétrie centrale.

Construction à la règle et au compas du symétrique d'un point:

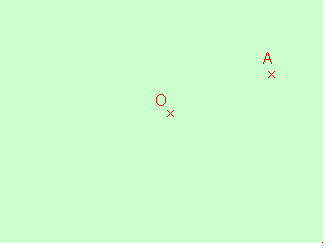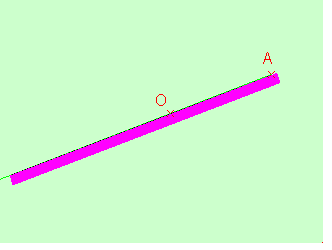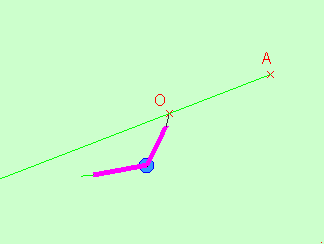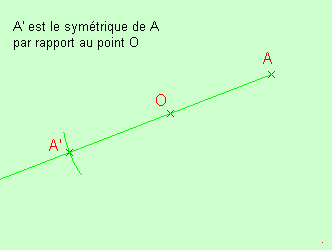
Remarques:

On considère une symétrie centrale de centre O.

1. Un seul point a pour symétrique lui-même: le point O. On dit que le point O est invariant par la symétrie de centre O. O est appelé le centre de symétrie.

2. Si A' est le symétrique de A par rapport à O, alors A est le symétrique de A' par rapport à O.

Une symétrie de centre O correspond à un demi-tour autour de O. Deux figures symétriques sont superposables.

On dit que:

La figureest le symétrique de la figure par rapport au point O;

ou encore que:

Les figures et sont symétriques par rapport au point O.

Propriété (admise): Le symétrique d'une droite d par rapport à un point O est:

• si O n'est pas sur d, une droite strictement parallèle à d.

• si O est sur d, la droite d elle-même. On dit dans ce cas que la droite d est globalement invariante par la symétrie de centre O.

Cas où :

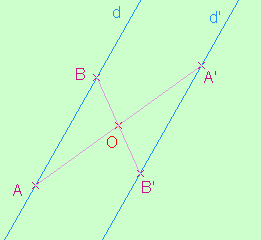
Cas où :

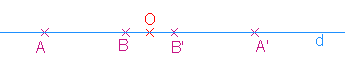
Conséquence: Si trois points sont alignés, alors leurs symétriques sont alignés.

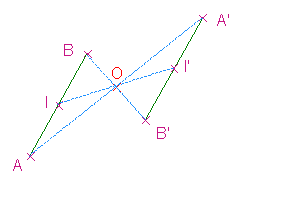
Propriété (admise): Le symétrique d'un segment par rapport à un point O est un segment de même longueur et à support parallèle.

De plus, le symétrique du milieu d'un segment est le milieu du segment symétrique.

Définition: On dit qu'une figure admet un point comme centre de symétrie si chaque point de la figure a son symétrique par rapport à ce point sur la figure elle-même.