Nombres relatifs. Repérage.

Les nombres négatifs sont notés avec le signe moins « - ». Ils sont plus petits ou égaux à zéro.

Exemple :-3 ; -5 ; -12,5 ; -520.

Les nombres positifs sont notés avec le signe plus « + ». Ils sont supérieurs ou égaux à zéro.

Exemple :+4 ; +6 +32,5 ; +520.

0 est le seul nombre qui est à la fois positif et négatif.

L’ensemble des nombres positifs et des nombres négatifs forme l’ensemble des nombres relatifs.

Un nombre relatif est déterminé par son signe ( + ou -) et par sa distance à zéro.

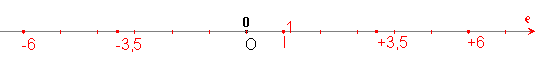
La distance à zéro de –6 est 6.

La distance à zéro de +6 est 6.

+6 et –6 sont des nombres relatifs opposés. De même –3,5 et 3,5.

Deux nombres relatifs sont dits opposés s’ils ont :

• des signes contraires ;

• la même distance à zéro.

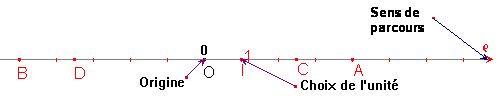
Une droite graduée (ou axe) est une droite sur laquelle on a choisi :

• une origine ;

• une unité

• un sens de parcours.

Chaque point d’une droite graduée peut être repéré par un nombre relatif appelé abscisse du point.

Point	A	B	C	D	O	I
Abscisse	+ 4	- 5	+2.5	-3.5	0	1

On note A (+4) ; B(-5).

Un repère orthogonal est constitué de deux droites graduées perpendiculaires de même origine. L’axe horizontal est appelé l’axe des abscisses et l’axe vertical l’axe des ordonnées.

Chaque point du plan est repéré par deux nombres relatifs appelés coordonnées du point. Le premier cité est toujours l’abscisse et le second est l’ordonnée.

Exemple: Sur la figure précédente, on a: A (4 ; 2).

Points	A	C	D	E	O	I	J
Coordonnées	(4 ;2)	(3 ;-2)	(-3 ;-1)	(-2 ;3)	(0 ;0)	(1 ;0)	(0 ;1)

Règles: - Si deux nombres sont négatifs, le plus petit est celui qui a la plus grande distance à zéro.
            - Si deux nombres sont de signes contraires, le plus petit est le nombre négatif.
            - Si deux nombres sont positifs, on sait déjà les comparer.