Correction de l'épreuve du brevet Session Juin 2003
Activités numériques
Exercice 1:
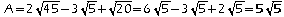 .
.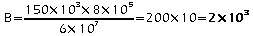
Exercice 2:
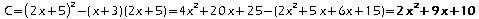 .
.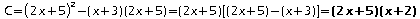 .
.-
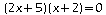 donne
donne
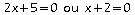 c'est
à dire:
c'est
à dire: 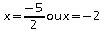 .
Les solutions de C = 0 sont
.
Les solutions de C = 0 sont 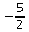 et
-2.
et
-2. Pour
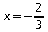 ,
on a:
,
on a:
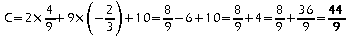
Exercice 3:
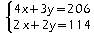
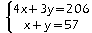
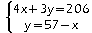
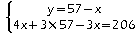
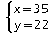
Vérification: ...
Le système a pour solution (35;22)
Soit x le prix en euros d'une place adulte et y celui d'une place enfant. Pour déterminer x et y, on obtient le système suivant:
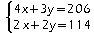 que
l'on a résolu à la question 1. Le prix d'une place
adulte est donc de 35 euros et celui d'une place enfant de 22 euros.
que
l'on a résolu à la question 1. Le prix d'une place
adulte est donc de 35 euros et celui d'une place enfant de 22 euros.Par suite la famille C paiera:
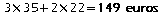 .
.
Travaux géométriques.
Exercice 1:
Dans les triangles ABE et ECD, on a: (AB)//(CD),
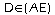 et
et
 ,
donc d'après le théorème direct de Thalès:
,
donc d'après le théorème direct de Thalès:
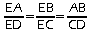 .
.Par suite:
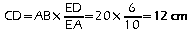 .
.Dans les triangles BFG et ABE, on a:
Les points B,F et E d'une part et B, G et A d'autre part, alignés dans le même ordre;
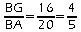 et
et
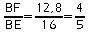 ,
d'où:
,
d'où:
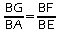 .
.Et donc d'après le théorème réciproque de Thalès, on a: (GF)//(AE).
Exercice 2:
Dans le triangle SOA rectangle en O, on a d'après le théorème direct de Pythagore:
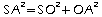 d'où:
d'où:
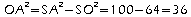 d'où:
d'où:
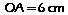
On a:
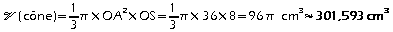 .
.Dans le triangle OAS rectangle en O, on a:
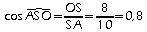 d'où:
d'où:
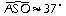 .
.a. Le coefficient k de cette réduction est donné par le rapport
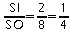 .
.b. On a:
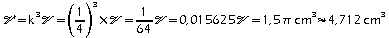 .
.
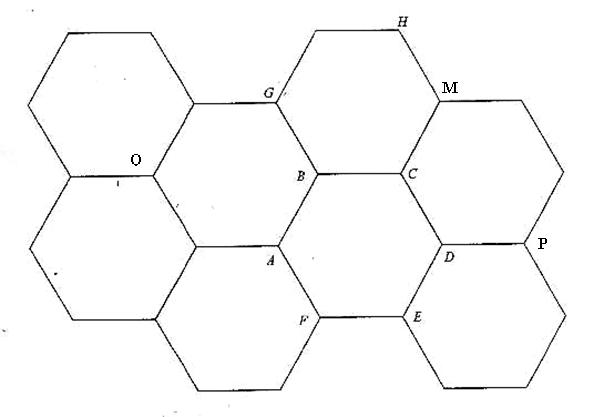
Problème:
Partie 1:
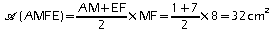 et
et
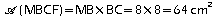 .
.a.
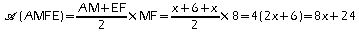 .
.b.
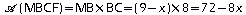
-
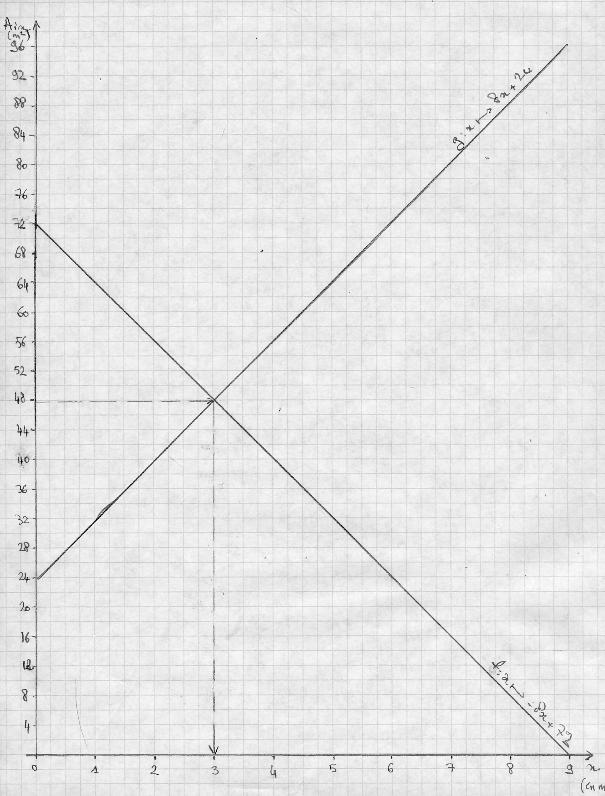
a. Graphiquement, on lit que:
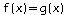 pour
pour
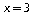 .
.b. On cherche la valeur de x telle que:
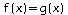 c'est
à dire telle que:
c'est
à dire telle que:
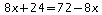 d'où:
d'où:
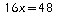 d'où
d'où
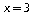 .
.
Partie 2:
Pour x = 3,5, on a: MB = 550 cm et BC = 800 cm.
a. c doit à la fois diviser 800 et 550, c'est donc un diviseur commun à ces deux nombres. Il est entier et le plus grand possible donc c'est le PGCD de 800 et 550.
b. En utilisant la méthode des divisions successives, on obtient:
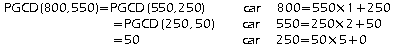
c. Il faut donc
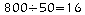 dalles
en longueur et
dalles
en longueur et
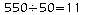 dalles
en largeur, soit
dalles
en largeur, soit
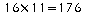 dalles
pour couvrir la salle de travail.
dalles
pour couvrir la salle de travail.La salle de travail a une surface de:
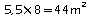 ,
d'où le prix à payer:
,
d'où le prix à payer: