Correction de l'épreuve de Mathématiques du DNB 2004
Activités numériques
Exercice 1:
Exercice 2:
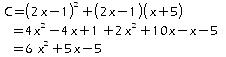 2.
2.
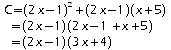
3.
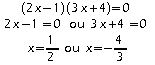
Exercice 3:
Les nombres 682 et 352 sont tous les deux divisibles par 2, leur PGCD est donc strictement supérieur à 1 et par conséquent ces deux nombres ne sont pas premiers entre eux.
Par la méthode des divisions successives:
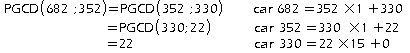
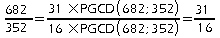 .
.
Exercice 4:
Il y a 2 + 5 + 2 + 2 + 3 + 2 + 7 + 2 = 25 élèves dans cette classe.
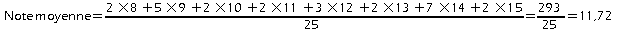
La note médiane se situe à la
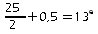 place
de la série statistique ordonnée, c'est à dire
correspond à la note 12.
place
de la série statistique ordonnée, c'est à dire
correspond à la note 12.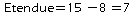 .
.
Activités géomériques
Exercice 1:
Dans les triangles MOU et MAI, on a:
les points O, M et A d'une part et les points U, M et I d'autre part alignés dans le même ordre.
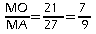 et
et
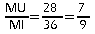 d'où:
d'où:
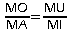 et
donc d'après le théorème réciproque de
Thalès, on a:
et
donc d'après le théorème réciproque de
Thalès, on a:
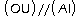 et
de plus:
et
de plus:
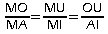 .
.On en déduit que:
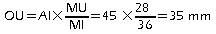
Dans le triangle AMI, on a:
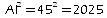 et
et
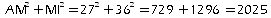 ,
d'où:
,
d'où:
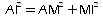 et
donc d'après le théorème réciproque de
Pythagore, le triangle AMI est resctangle en M.
et
donc d'après le théorème réciproque de
Pythagore, le triangle AMI est resctangle en M.Dans le triangle AMI rectangle en M, on a:
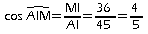 d'où:
d'où:
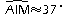 .
.Les angles
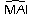 et
et
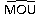 sont
alternes internes. De plus les droites (OU) et (AI) sont parallèles,
donc ces angles ont la même mesure.
sont
alternes internes. De plus les droites (OU) et (AI) sont parallèles,
donc ces angles ont la même mesure.
Exercice 2:
a. Construction de
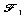 et
placement de E image de A.
et
placement de E image de A.b. Construction de
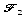 et
placement de T image de E.
et
placement de T image de E.On peut passer de la figure
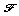 à
la figure
à
la figure
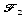 directement
par la translation de vecteur
directement
par la translation de vecteur
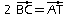
Exercice 3:
Le triangle ABC est isocèle en A. Comme (AO) est la hauteur principale de ce triangle, elle passe par le milieu O de [BC], et donc
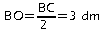 .
Par suite dans le triangle AOB rectangle en O, on a, d'après
le théorème direct de Pythagore:
.
Par suite dans le triangle AOB rectangle en O, on a, d'après
le théorème direct de Pythagore:
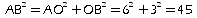 d'où:
d'où:
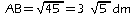 .
.a.
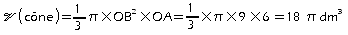
b.
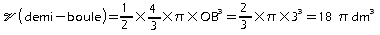
c.
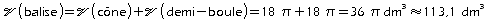
Problème
Partie 1:
Construction du triangle.
a.
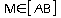 d'où:
d'où:
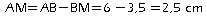 .
.b. On a:
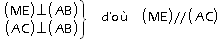 .
.c. Dans les triangles BME et BAC, on a:
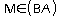 ,
,
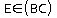 et
et
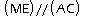 donc
d'après le théorème direct de Thalès:
donc
d'après le théorème direct de Thalès:
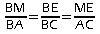 ,
d'où:
,
d'où:
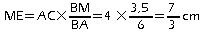 .
.d. On a:
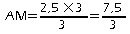 d'où:
d'où:
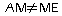 et
donc le triangle AME n'est pas isocèle en M.
et
donc le triangle AME n'est pas isocèle en M.
Partie 2:
Dans les triangles BME et BAC, on a:
 ,
,
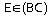 et
et
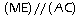 donc
d'après le théorème direct de Thalès:
donc
d'après le théorème direct de Thalès:
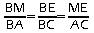 ,
d'où:
,
d'où:
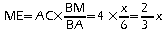 .
.a.
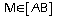 d'où:
d'où:
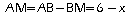 .
.b. On cherche x tel que le triangle AME soit isocèle en M, c'est à dire tel que
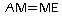 .
Autrement dit on cherche x tel que:
.
Autrement dit on cherche x tel que: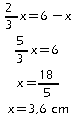
La valeur de x tel que AME soit un triangle isocèle en M est 3,6 cm.
a. f est une fonction linéaire. La représentation graphique de f est une droite qui passe par le point de coordonnées (0;0) . On a:
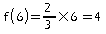 et
donc la représentation graphique de f passe par le point de
coordonnées (6;4).
et
donc la représentation graphique de f passe par le point de
coordonnées (6;4).g est une fonction affine. La représentation graphique de g est donc une droite. On a:
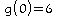 et
et
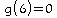 .
La représentation graphique de g passe donc par les points de
coordonnées
.
La représentation graphique de g passe donc par les points de
coordonnées
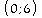 et
et
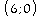 .
.
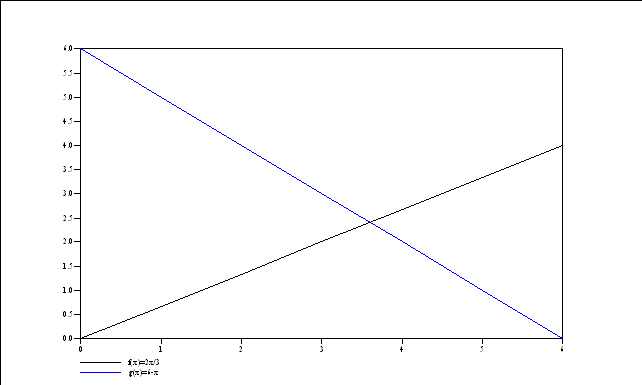
b.
Graphiquement, on lit: x = 3,6 cm comme abscisse du point
d'intersection des deux droites, c'est à dire la valeur de x
telle que:
![]() qui
répond au problème posé.
qui
répond au problème posé.
