Correction de l'épreuve de mathématiques du DNB
session de Juin 06

Exercice 1:

1.

2.

3.

Exercice 2:

1. 

2. 

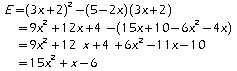
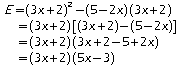
3. Pour 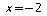, on a:

4. 

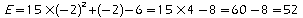
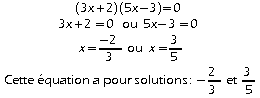
Exercice 3:

1. Pour x = 2 et y = 0,5, on a:

et: donc le couple (2; 0,5) n'est pas solution du système

2.

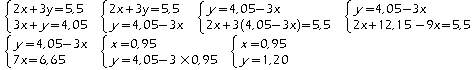
Vérification:Pour x=0,95 et y=1,20 on a:

et donc le système a pour solution le couple (0,95;1,2).

3. Soit x le prix d'un croissant et y celui d'un pain au chocolat. De l'énoncé, on déduit que: et donc qu'un croissant coûte 0,95 euros et un pain au chocolat 1,20 euros.

Exercice 1:

1. Dans le triangle PBM, on a:

et , d'où: et donc d'après le théorème réciproque de Pythagore, le triangle PBM est rectangle en M.

2. Dans le triangle PBM rectangle en M, on a: d'où: .

3. Dans les triangles PBM et PNS, on a: , et , donc d'après le théorème direct de Thalès, on a: .

Par suite: .

4. Dans les triangles PCE et PMB, on a:

les points P,C et M d'une part et les points P,E et B d'autre part, alignés dans le même ordre.

et d'où: .

Donc d'après le théorème réciproque de Thalès: (CE)//(MB).

Exercice 2:

1. et 2.a Voir figure

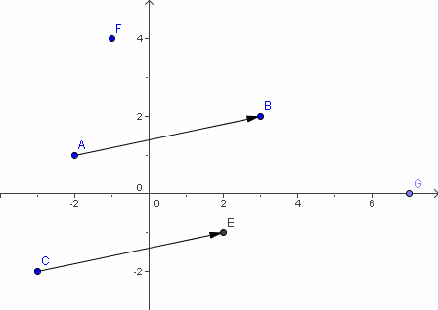
2.b. Le point E a pour coordonnées (2,-1).

3.

4. Soit I le milieu de [CF], on a: et

Or A(-2;1), donc I et A sont confondus et par suite A est le milieu de [CF] et donc F est le symétrique de C par rapport à A.

5. Soit J le milieu de [FG] . On a: et . Or B(3;2), donc B et J sont confondus et donc B est le milieu de [FG].

Par suite dans le triangle FCG, on a: A est le milieu de [CF] et B est le milieu de [FG] donc d'après le théorème direct des milieux, (AB)//(CG) et donc

Partie A

1.

2. a)

b)

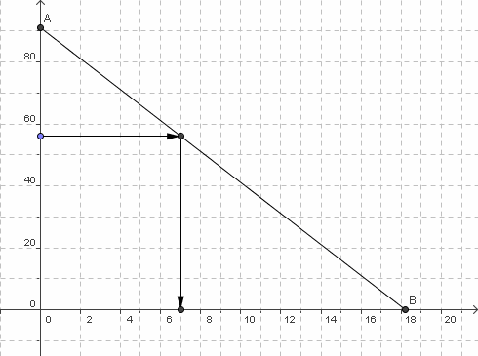
c) Graphiquement, le nombre d'heures nécessaires pour qu'il ne reste plus que dans la piscine est de 7 heures.

d) Graphiquement la piscine sera vide lorsque la représentation graphique de f rencontre l'axe des abscisses, en le point B, soit au bout de 18,2 h.

e) On cherche la valeur de x telle que f(x)=0, c'est à dire telle que 91-5x=0, soit , d'où:, ce qui donne un temps de 18h et 12 min.

Partie B

1. et .

2. Comme il veut un nombre entier de panneaux de longueur a, celle ci-doit diviser chacune des longueurs de clôture, donc a doit être un diviseur commun à 750 et 1650, le plus grand possible, ce qui correspond au PGCD des deux nombres.

3. On utilise l'algorithme d'Euclide:

4. Il faudra donc: